STL std::sort是什么样的排序?
1000 Words | Read in about 5 Min | View times
Overview
排序是最基础的一种算法,C++的STL标准库也提供了一些关于排序算法的实现,其中使用最多的当属std::sort()了,也是工作面试中的高频主角。本节内容将对std::sort()具体的源码实现进行详细解剖。
本系列文章将包括以下领域:
本章其他内容请见 《现代C++》
背景
从事计算机程序设计的同学一定对排序非常熟悉,自从我们接触数据结构与算法课程的时候便伴随我们左右。任何一本关于数据结构与算法的课程都会介绍各种各样的排序算法,其中最著名的当属快速排序。既然是以“快速”命名的排序算法,它的平均时间复杂度可以达到O(nlogn),是最快排序算法之一。
在各种面试中,一问算法必涉及排序,一问排序必涉及快速排序。那么STL标准库实现的std::sort()算法,是快速排序算法吗?
答案是不完全是,快速排序只是std::sort()算法1/3的内容,还有其他排序算法结合实现。
C++标准库向来以极致的高性能著称,快速排序虽然以快速著称,但是它也有一大堆问题需要解决。所以std::sort()不会是简单的快速排序。
快速排序的问题
那么快速排序有什么哪些问题呢?
-
数据量大或者数据量小都适合快速排序吗?
-
快速排序可能由于pivot选择不当,导致其最坏时间复杂度恶化为
O(n^2),怎么解决这种最坏的情况? -
快速排序一般是递归实现的,递归是一种函数调用,对栈帧空间要求较高,递归深度过大效率大大下降,怎么解决这种情况?
-
怎么控制递归深度?达到递归深度了还没排序完成怎么办?
那么在常见的算法实现中,其他算法能不能解决这些问题呢?
答案是可以的,利用各种排序算法的优势,结合在一起就能解决。比如插入排序就适合数据量小的排序,堆排序在最优、最差和平均的时间复杂度都是O(nlogn)。
插入排序的优点
插入排序对基本有序的情况表现非常好。在StackOverflow上有关于这个问题的讨论 Which sort algorithm works best on mostly sorted data?。
堆排序的优点
堆排序和快速排序的平均时间复杂度都是O(nlogn),虽然复杂度一样,但是堆排序的时间常数要比快速排序大。这里有关于堆排序缺点的讨论 《堆排序缺点何在?》。
但是堆排序最坏情况的时间复杂度依旧是O(nlogn)。
内省式排序
综合快速排序、插入排序和堆排序三种排序方法的优点,有人提出了内省式排序(introspective sorting):
-
在数据量大的时候采快速排序,此时时间复杂度为
O(nlogn) -
一旦分段后的数据量小于某个阈值,就改用插入排序,此时分段基本有序,此时时间复杂度为
O(n) -
在快排递归过程中,如果递归深度超过某个阈值,分段就有恶化倾向,于是改用堆排序,此时维持时间复杂度为
O(nlogn)
std::sort的适用范围
并非所有容器都适合使用std::sort()算法。关联容器都拥有内部的排序功能,比如std::map底层使用红黑树实现,自带排序功能了,所以不需要std::sort()。容器适配器都有特定的出入口,是不能排序的,比如std::stack不允许排序。剩下的顺序容器如vector、deque等是可以使用std::sort()算法的。
std::sort的源码剖析
std::sort的实现基本上就是采用内省式排序的策略。接下来我们通过对源码的剖析来理解整个算法的实现思路。
std::sort是实现位于头文件<stl_algo.h>。
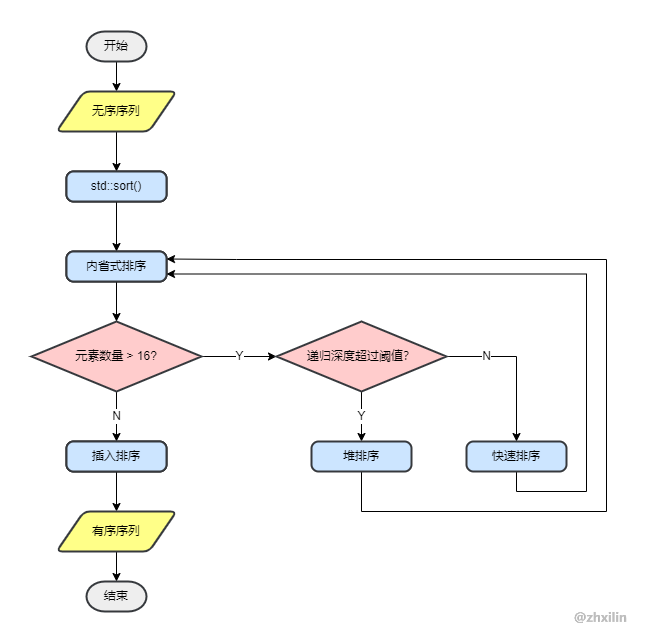
先通过一张图简单了解一下std::sort的结构:

std::sort入口
1//<stl_algo.h>
2template<typename _RandomAccessIterator>
3constexpr inline void sort(_RandomAccessIterator __first, _RandomAccessIterator __last)
4{
5 // concept requirements
6 __glibcxx_function_requires(_Mutable_RandomAccessIteratorConcept<_RandomAccessIterator>)
7 __glibcxx_function_requires(_LessThanComparableConcept<typename iterator_traits<_RandomAccessIterator>::value_type>)
8 __glibcxx_requires_valid_range(__first, __last);
9 __glibcxx_requires_irreflexive(__first, __last);
10
11 //核心入口
12 std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
13}
14
15template<typename _RandomAccessIterator, typename _Compare>
16constexpr inline void __sort(_RandomAccessIterator __first, _RandomAccessIterator __last, _Compare __comp)
17{
18 if (__first != __last)
19 {
20 //内省式排序
21 std::__introsort_loop(__first, __last, std::__lg(__last - __first) * 2, __comp);
22 //插入排序
23 std::__final_insertion_sort(__first, __last, __comp);
24 }
25}
26
27//<predefined_ops.h>
28struct _Iter_less_iter
29{
30 template<typename _Iterator1, typename _Iterator2>
31 constexpr bool operator()(_Iterator1 __it1, _Iterator2 __it2) const
32 {
33 return *__it1 < *__it2;
34 }
35};
36
37constexpr inline _Iter_less_iter __iter_less_iter()
38{
39 return _Iter_less_iter();
40}
std::sort的核心入口是std::__sort,只要范围有效,就会调用std::__introsort_loop和std::__final_insertion_sort。
std::__introsort_loop就是大名鼎鼎的内省式排序;std::__final_insertion_sort就是插入排序。
std::__introsort_loop内省式排序框架
来看一下内省式排序的核心框架:
1//<stl_algo.h>
2enum { _S_threshold = 16 };
3
4template<typename _RandomAccessIterator, typename _Size, typename _Compare>
5constexpr void __introsort_loop(_RandomAccessIterator __first,
6 _RandomAccessIterator __last,
7 _Size __depth_limit,
8 _Compare __comp)
9{
10 while (__last - __first > int(_S_threshold))
11 {
12 if (__depth_limit == 0)
13 {
14 //堆排序
15 std::__partial_sort(__first, __last, __last, __comp);
16 return;
17 }
18 //快速排序
19 --__depth_limit;
20 //快排-分割
21 _RandomAccessIterator __cut = std::__unguarded_partition_pivot(__first, __last, __comp);
22 //快排-右侧递归
23 std::__introsort_loop(__cut, __last, __depth_limit, __comp);
24 //快排-调整右边界到分割点,下一次循环就是左侧递归
25 __last = __cut;
26 }
27}
当数据量大于阈值_S_threshold,即超过16个元素时,进入循环。
递归深度__depth_limit的默认值为std::__lg(__last - __first) * 2,用来控制快速排序的分割恶化。循环每进行一次,递归深度递减一层。
回忆一下快排的基本思路:选定轴pivot,以轴为分割点,对数据进行分割,小于分割点的移到左边,大于分割点的移到右边;递归处理分割点左侧部分;递归处理分割点右侧部分。
在这里,调用快排的分割函数std::__unguarded_partition_pivot对数据进行分割,得到分割点cut。接下来开始对分割点右侧部分进行递归,再次调用std::__introsort_loop。
注意看这里为什么左侧部分没有进行递归呢?
这是因为当右侧递归结束后,__last = __cut将终点调整到了分割点,此时剩下的部分就是原来序列的左侧部分,所以下次循环递归处理就完了。也正是因为快排一次完整的过程需要进入两次while循环,所以递归深度的默认值有一个* 2的计算。一次完整的快排递归扣减了两次__depth_limit。这种做法的好处是,有一半的数据处理直接通过循环就能进行,没必要进行函数调用,因为函数调用又有一定函数调用堆栈的开销。虽然可读性降低了,但是性能却得到了提升了,再次印证了C++标准库为了提高效率使出了各种手段。
当__depth_limit被减为0之后,就停止递归,而是进入std::__partial_sort,这里就是堆排序了。堆排序结束之后直接结束递归。
std::__unguarded_partition_pivot快排分割
我们继续把目光聚焦在快排上。看一下快排的分割算法实现:
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr inline _RandomAccessIterator __unguarded_partition_pivot(_RandomAccessIterator __first,
4 _RandomAccessIterator __last,
5 _Compare __comp)
6{
7 _RandomAccessIterator __mid = __first + (__last - __first) / 2;
8 //三点中值法
9 std::__move_median_to_first(__first, __first + 1, __mid, __last - 1, __comp);
10 //真正的分割算法
11 return std::__unguarded_partition(__first + 1, __last, __first, __comp);
12}
13
14template<typename _Iterator, typename _Compare>
15constexpr void __move_median_to_first(_Iterator __result,_Iterator __a, _Iterator __b, _Iterator __c, _Compare __comp)
16{
17 if (__comp(__a, __b))
18 {
19 if (__comp(__b, __c))
20 std::iter_swap(__result, __b);
21 else if (__comp(__a, __c))
22 std::iter_swap(__result, __c);
23 else
24 std::iter_swap(__result, __a);
25 }
26 else if (__comp(__a, __c))
27 std::iter_swap(__result, __a);
28 else if (__comp(__b, __c))
29 std::iter_swap(__result, __c);
30 else
31 std::iter_swap(__result, __b);
32}
33
34template<typename _RandomAccessIterator, typename _Compare>
35constexpr _RandomAccessIterator __unguarded_partition(_RandomAccessIterator __first,
36 _RandomAccessIterator __last,
37 _RandomAccessIterator __pivot,
38 _Compare __comp)
39{
40 while (true)
41 {
42 while (__comp(__first, __pivot))
43 ++__first;
44
45 --__last;
46
47 while (__comp(__pivot, __last))
48 --__last;
49
50 if (!(__first < __last))
51 return __first;
52
53 std::iter_swap(__first, __last);
54 ++__first;
55 }
56}
首先std::__move_median_to_first的作用是把三个值的中间值选出来作为pivot,pivot的位置挪到序列的开头。我们常规的选取pivot的做法是选择首、尾或中间值作为分割点,并不会比较它们的值。而三值中点法优于传统的分割点选取方式,可以更好地避免出现分割失误导致的递归恶化。
std::__unguarded_partition是真正的分割逻辑,以pivot为轴将数据划分为两部分。它会不断去交换放错位置的元素,直到__first和__last指针相互交错为止,函数返回的是右边区间的起始位置。注意这个函数没有对__first和__last作边界检查,而是以两个指针交错作为中止条件,节约了比较运算的开销。这是因为,选择是三值中间点作为pivot,因此一定会在超出此有效区域之前结束指针的移动,故函数名也以__unguarded开头。
这里需要特别注意__comp的比较关系,必须符合严格弱序关系,即__comp(a, a)必须等于false。假设不遵守严格弱序关系,即__comp(a, a) == true,在std::__unguarded_partition中执行到while (__comp(__first, __pivot))时,while循环一直返回true,会导致__first一直右移直到越界;同理while(__comp(__pivot, __last))也一样,会一直左移直到越界。因此这种情况下会引起coredump。
关于严格弱序关系,cppreference是这么描述的:
建立具有下列性质的严格弱序关系
- 对于所有 a,comp(a,a)==false
- 若 comp(a,b)==true 则 comp(b,a)==false
- 若 comp(a,b)==true 且 comp(b,c)==true 则 comp(a,c)==true
这是在传入自定义谓词比较器的时候容易出现的隐藏bug,需要特别小心。
std::__partial_sort堆排序
前面讲到当递归深度超过一定层数,就开始改用堆排序:
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr inline void __partial_sort(_RandomAccessIterator __first,
4 _RandomAccessIterator __middle,
5 _RandomAccessIterator __last,
6 _Compare __comp)
7{
8 //在区间[__first, __middle)建堆,并使[first, __middle)区间存放前__middle - first个最小值
9 std::__heap_select(__first, __middle, __last, __comp);
10 //对[__first, __middle)区间进行堆排序
11 std::__sort_heap(__first, __middle, __comp);
12}
13
14template<typename _RandomAccessIterator, typename _Compare>
15constexpr void __heap_select(_RandomAccessIterator __first,
16 _RandomAccessIterator __middle,
17 _RandomAccessIterator __last,
18 _Compare __comp)
19{
20 //在区间[__first, __middle)建堆
21 std::__make_heap(__first, __middle, __comp);
22 //使[first, __middle)区间存放前__middle - first个最小值
23 for (_RandomAccessIterator __i = __middle; __i < __last; ++__i)
24 if (__comp(__i, __first))
25 std::__pop_heap(__first, __middle, __i, __comp);
26}
27
28template<typename _RandomAccessIterator, typename _Compare>
29constexpr void __sort_heap(_RandomAccessIterator __first,
30 _RandomAccessIterator __last,
31 _Compare& __comp)
32{
33 //堆排序
34 while (__last - __first > 1)
35 {
36 --__last;
37 std::__pop_heap(__first, __last, __last, __comp);
38 }
39}
std::__partial_sort函数取出[__first, __last)区间前__middle - _frist个最小元素,并将其按照比较策略进行排序后,有序存放在[__first, __middle)区间,其余的节点仍是无序地放在[__middle, __last)区间。
而在std::__introsort_loop中调用std::__partial_sort时传入的__middle参数其实是__last:
1std::__partial_sort(__first, __last, __last, __comp);
相当于在[__first, __last)全区间进行了堆排序。通过堆排序,可以把恶化的快排时间复杂度O(n^2)提升到O(nlogn)。
std::__final_insertion_sort插入排序
最后是插入排序:
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr void __final_insertion_sort(_RandomAccessIterator __first,
4 _RandomAccessIterator __last,
5 _Compare __comp)
6{
7 if (__last - __first > int(_S_threshold))
8 {
9 //先处理前16个元素
10 std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
11 //剩余元素
12 std::__unguarded_insertion_sort(__first + int(_S_threshold), __last, __comp);
13 }
14 else
15 std::__insertion_sort(__first, __last, __comp);
16}
插入排序分为两部分处理,第一个分支是处理超过16个元素的情况,第二个分支是处理小于等于16个元素的情况。第一个分支还分成两段处理:小于16个元素的部分,和剩余部分。
看完这段代码一定会产生几个疑问:
为什么要分成两个分支处理?
为什么第一个分支还要分成两段?
__insertion_sort和__unguarded_insertion_sort有什么区别?
核心问题是第三个问题,解决了这个问题,前面两个问题就迎刃而解了。我们带着这些疑问接着往下看。
在维基百科里,插入排序的伪代码是这样的:
1i ← 1
2while i < length(A)
3 j ← i
4 while j > 0 and A[j-1] > A[j]
5 swap A[j] and A[j-1]
6 j ← j - 1
7 end while
8 i ← i + 1
9end while
可以看到,从第二个元素开始遍历,首先要判断是否越界,然后判断是否需要交换。而__insertion_sort是怎么实现的呢?
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr void __insertion_sort(_RandomAccessIterator __first,
4 _RandomAccessIterator __last, _Compare __comp)
5{
6 if (__first == __last) return;
7
8 for (_RandomAccessIterator __i = __first + 1; __i != __last; ++__i)
9 {
10 if (__comp(__i, __first))
11 {
12 typename iterator_traits<_RandomAccessIterator>::value_type __val = std::move(*__i);
13 //将排好序的部分整体后移一位
14 std::move_backward(__first, __i, __i + 1);
15 *__first = std::move(__val);
16 }
17 else
18 std::__unguarded_linear_insert(__i, __gnu_cxx::__ops::__val_comp_iter(__comp));
19 }
20}
21
22template<typename _RandomAccessIterator, typename _Compare>
23constexpr void __unguarded_linear_insert(_RandomAccessIterator __last, _Compare __comp)
24{
25 typename iterator_traits<_RandomAccessIterator>::value_type __val = std::move(*__last);
26 _RandomAccessIterator __next = __last;
27 --__next;
28 while (__comp(__val, __next))
29 {
30 *__last = std::move(*__next);
31 __last = __next;
32 --__next;
33 }
34 *__last = std::move(__val);
35}
在std::__insertion_sort的从第二个元素开始遍历,仔细看循环中的部分,每个元素会先跟第一个元素作比较,满足比较条件的时直接将前面已经排好序的数据整体向后移动一位,然后把该元素放在第一位。与标准的实现过程相比,将__last - __first - 1次比较操作直接用一次std::move_backward替代,节省了每次移动前的比较。
如果不满足比较条件,则调用std::__unguarded_linear_insert,这里仅仅是从后往前逐个判断是否需要交换,找到位置后就将其插入该位置。注意这里没有判断任何越界问题,为什么可以不用判断?因为在std::__insertion_sort的循环中,if分支中已经保证了左边范围内一定有排序后的第一个值了,即第一个值已经在最左边,所以当进入else分支后就没必要再进行边界检查了。所以又节省了多次比较。也正因为没有判断边界,函数以__unguarded开头。
std::__insertion_sort到这儿就讲完了,接下来再看std::__unguarded_insertion_sort又有什么不同:
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr inline void __unguarded_insertion_sort(_RandomAccessIterator __first,
4 _RandomAccessIterator __last,
5 _Compare __comp)
6{
7 for (_RandomAccessIterator __i = __first; __i != __last; ++__i)
8 std::__unguarded_linear_insert(__i, __gnu_cxx::__ops::__val_comp_iter(__comp));
9}
这个函数只是直接对每个元素都调用std::__unguarded_linear_insert而已。前面已经分析过std::__unguarded_linear_insert了,它不对边界作检查。因此std::__unguarded_insertion_sort一定比std::__insertion_sort快,但前提是保证调用std::__unguarded_linear_insert前序列的左侧部分已经有了有序序列的第一个值了。
到这里我们已经介绍完std::__insertion_sort和std::__unguarded_insertion_sort的区别了,我们回头再来看看之前提出的三个疑问:
为什么要分成两个分支处理?
为什么第一个分支还要分成两段?
__insertion_sort和__unguarded_insertion_sort有什么区别?
第三个问题已经解答,我们看看前两个问题。为了加深印象,我们再看一下std::__final_insertion_sort的实现:
1//<stl_algo.h>
2template<typename _RandomAccessIterator, typename _Compare>
3constexpr void __final_insertion_sort(_RandomAccessIterator __first,
4 _RandomAccessIterator __last,
5 _Compare __comp)
6{
7 if (__last - __first > int(_S_threshold))
8 {
9 std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
10 std::__unguarded_insertion_sort(__first + int(_S_threshold), __last, __comp);
11 }
12 else
13 std::__insertion_sort(__first, __last, __comp);
14}
最外层分成两个分支,分别处理超过16个元素和小于等于16个元素。对于小于等于16个元素,直接使用std::__insertion_sort就可以了,没有必要进行复杂的划分。注意这里面会进行边界检查。
重点是超过16个元素的部分,需要采用一定策略让这部分的排序效率最大化,所以进行了前16个元素的划分。先对前16个元素进行一次std::__insertion_sort,含有边界检查,保证了整个序列中前16个元素是有序的;对于剩余部分,就可以直接调用std::__unguarded_insertion_sort,不作任何边界检查,因为这个函数要求它的序列的左侧部分有序且有第一个值。如此一来对超过16个元素的数据分成两段处理,都能各自发挥性能优势,效率最大化,何乐而不为?
至此,三个疑问都得到了解答。